ein gnomon ist eine spezielle form eines parallelogramms. und zwar folgendermassen definiert:

"... Figur, die entsteht, wenn man aus einem Parallelogramm ein ihm ähnliches und ähnlich gelegenes so ausschneidet, daß es eine Ecke mit dem ursprüngl. Parallelogramm gemeinsam hat." (quelle: antike probleme)

ein gnomon ist aber auch ...
"...ein bereits von den Babyloniern zu astronom. Zwecken verwendeter Stab, dessen unterschiedl. Schattenlänge zur Bestimmung der Sonnenwenden und der Tagundnachtgleichen diente." (quelle: antike probleme)

somit sind 2 antworten richtig: (B) und (C)
- erste(r) ist engraver mit der völlig korrekten anwort.
- zweite(r) ist boomerang mit einer teilantwort
- dritte(r) ist eria mit einer teilantwort

und einen anerkennungspreis bekommt culwen, der auf meinen lösungsvorschlag (F) getippt hat :-)).

danke auch an walküre und T.C. fürs mitraten.

ich werde euch ein paar antwortmöglichkeiten geben und, weil ich so nett bin, die richtige(n) drunter mischen.


a) ein charakteristisches mathematisches ergebnis
b) ein spezielles parallelogramm
c) ein stab, der schatten wirft
d) ein geschwür in der dickdarm-gegend
e) eines der letzten stadien, bevor ein stern explodiert
f) ein zwerg, der dauernd im internet surft

Die öffentlichen Büchereien meldeten 2002 17,0 Millionen Entlehnungen bei 1,1 Millionen registrierten Lesern.

Wieviele Bücher wurden im Jahr 2002 von den 1,1 Millionen registrierten Lesern aus öffentlichen Bibliotheken entliehen?

wie poons (als einziger!) schon ganz richtig festgestellt hat, läuft das folgendermaßen ab:

ein paar fährt gemeinsam über den fluss. dann fährt die frau wieder zurück und holt eine andere frau auf die andere seite des flusses. dort steigt dann die frau aus, deren mann schon auf dieser seite des flusses wartet. und das spiel beginnt von vorne.

die schritte nochmal im einzelnen:

1.) m1 und f1 überqueren den fluss
2.) f1 fährt zurück und holt f2
3.) f1 steigt aus und geht zu ihrem mann m1
4.) f2 fährt zurück und holt ihren mann m2
5.) f2 fährt nochmals zurück und holt die frau f3
6.) f2 steigt aus und geht zu ihrem mann m2
7.) f3 fährt nochmal zurück und holt ihren mann m3

nun sind alle paare auf der sonnigen seite und können ihren spaziergang fortsetzen :-)

auch heute gibts wieder etwas zum rätseln. folgende situation:

3 paare sind gemeinsam unterwegs, gehen so dahin und schon bald gelangen sie an einen fluss. auf der gegenüberliegenden seite ist alles so wunderbar, es scheint die sonne ganz hell und es schaut einfach toll aus. so beschliessen die 3 paare, dass sie den fluss überqueren wollen. schnell finden sie für dieses vorhaben auch ein floss, auf dem jedoch immer nur 2 personen platz haben.

es gibt dabei nur ein problem: alle frauen sind wunderschön und die männer so eifersüchtig, dass die eigene frau nie allein mit einem anderen mann irgendwo allein sein darf.

in welcher reihenfolge können sie nun den fluss mit dem floss überqueren?

ursprünglich beruht das problem auf einer geschichte, in der gott bei der welterschaffung 64 scheiben übereinander gestapelt hat und seine priester anwies, sie sollen den stapel auf eine andere diamantnadel verlagern. wenn die priester dies schaffen, würde alles zu staub zerfallen und die welt untergehen.

was die priester nicht wussten, war, dass die formel zur versetzung der scheiben: 2^n - 1 (2 hoch n, minus 1) lautet, n beschreibt die anzahl der scheiben. somit hätten wir bei 4 scheiben in unserem beispiel eine minimale zuganzahl von 15 zügen.

bei 64 scheiben sind es dann etwa 18.447.000.000.000.000.000 verschiebungen. wenn die mönche jede sekunde eine scheibe versetzen würden, würden sie 585 milliarden jahre arbeiten, bis das problem gelöst wäre :-) (is ja nix in bezug auf die ewigkeit).

wie die züge genau aussehen, könnt ihr an diesen applets selber beobachten:
- www.math.tu-berlin.de
- wanda.fh-aargau.ch

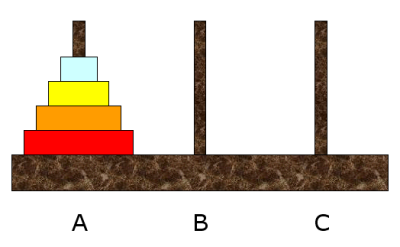
zuerst zur erklärung des problems: wir haben ein brett mit drei stiften, auf denen vier scheiben aufgespießt wurden. die scheiben liegen untereinander, man hat also immer nur zugriff auf die oberste scheibe. man kann nun frei die scheiben von einem turm (z.B. A) auf einen anderen turm (z.B. B oder C) setzen, wobei man immer beachten muss, dass stets kleinere scheiben auf größeren scheiben oder dem blanken brett liegen müssen!
es darf immer nur eine scheibe auf einmal bewegt werden!

und jetzt die frage: wieviel züge braucht man minimal, um alle scheiben des turms A auf den turm C zu übertragen?

in einer 500g packung sind gezählte 458 stück nudeln!

rahomil war am nächsten dran, super ;-) ich hab sie gezählt, werd aber wohl nicht mehr so schnell eine solche schätzfrage bringen *smile*